ClearMath
The Methodology
ClearMath
The Methodology
The ClearMath methodology thrives on growth mindset, expectation of excellence, and efficiency. Growth mindset is prevalent because the teacher can always teach a better lesson and the student can always learn more. Expectation of excellence is natural because mediocrity is not tolerated. Efficiency is accomplished because lessons are not taught in a linear format. Need determines the path. Inquiry-based dialogue and productive struggle are two major facets of the model.
This model of instruction and learning is not a cookie-cutter. Every student has unique needs that require tailored solutions. Often these unique needs cannot be anticipated. Therefore, spontaneity, enhanced by empathy and a solid understanding of the subject, is required. Since need is at the forefront and “teaching to the moment” comes into play, the parts of the model are not clearly partitioned and order is not sequenced.
Students should not be made to fit lessons…lessons should be made to fit students! Since every teaching situation is unique, it is best to think of teaching as a craft as opposed to assembly line work. Successful teaching depends on the craft of the teacher. The goal of ClearMath is to improve this craft by defining it better.
To define this pedagogy, successful teaching has been reverse-engineered.
The following overview defines the ClearMath model for instruction and learning.
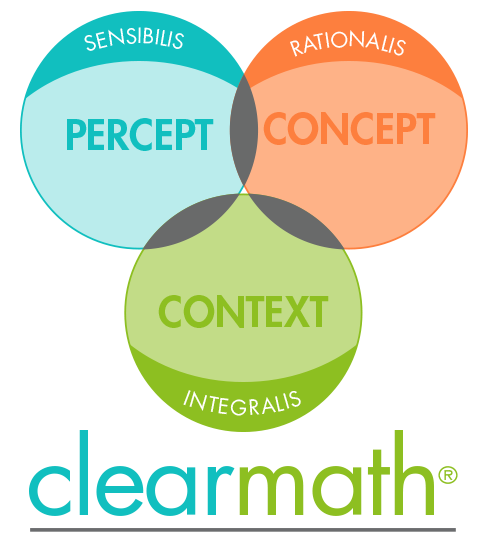
The three parts of this model are:
- Percepts (SENSIBILIS) – thoughts that are created from our senses of seeing and hearing…the “show and tell” environment (Perceptual Imperatives are recognized at this point. These are the conduits and catalysts that aid the birth of concepts.)
- Concepts (RATIONALIS) – ideas formed from the perceptions
- Context (INTEGRALIS) – the holistic or integrated part of the learning cycle (The word literally says, “weave together”. Concepts are woven together so that application and problem-solving can take place. Critical thinking is realized.)

Perceptual Imperatives...
Catalysts and conduits that give birth to concepts – The things we see and hear that aid conceptual understanding (There is not an all-inclusive list of perceptual imperatives)
Equivalence
Equivalence is probably the most used perception in mastering mathematical understanding. Equivalence is when two different looking expressions have the same value. The word, equivalent, is also used when two different looking variable sentences have the same solution set.
Forms of One
“Forms of One” aid the meaning of equivalent rational expressions. This gives meaning to the concept, multiplicative inverse (reciprocals). Making “Implied Ones” explicit, addresses possible early ambiguity.
Inverses
Inverses is a necessary percept in understanding the additive identity, “zero,” and the multiplicative identity, “one”.
Generalization
Generalization gives specificity contextual meaning…a way of seeing bigger, broader, and of course, more general. This percept gives use of variables more meaning and understanding. It gives the young math students a head start to algebraic reasoning.
Models
Models give visual representation to aid critical thinking and problem-solving. They might be in the form of the real number line, a picture chart, graph, diagram, table, drawing, or a mathematical expression or sentence.
Genre
Genre shows that consistent concepts can be connected to certain classifications.
Forms of Zero
“Forms of Zero” give meaning to the concept, additive inverse (opposites).
Math Properties
Math Properties give meaning to equivalence. These characteristics give a formal reason why different “looks” have the same value. They give the translation of language more meaning.
Math as a Language
Seeing Math as a Language facilitates the holistic understanding of its expression. Symbols, expressions, sentences, and the importance of vocabulary connect naturally when the percept of language is being created. As students get a better percept of the language, this gives more depth of understanding to their journey.
Arithmetic Operations
Arithmetic Operations are the counting percepts that lead to measurement and the idea of quantity. All arithmetic operations are binary and can be put into context with addition, after addition has been perceived.
Units
Units create relevance, consistency, and meaning in measurement and numerical operations.
Terms and Factors
The percept of Terms and Factors eliminates memorizing “rules” for “order of operations.” This percept gives in-depth concept understanding to mathematical expressions instead of relying on “rules”, rhymes, and algorithms that have no concept value.
Patterns
Patterns…recognizing consistent change such that prediction can be made.
ClearMath
Request More Information
For more information about our math tutoring/enrichment services for students and consulting services for math teachers and educators:

